★ 内接球とか4等分とか ★
正四面体を作ると、どうしても気になるのが、内接球です。よね??
高校の数学では、必ずと言っていいほど登場します。
でもまず、内接球って、どこに接してるのかが、判りにくい。
「え?辺じゃないの??ナンデ??」
と言う生徒がいる。
となると、やっぱり、断面が見たい。実際に触れて納得したい。
さらに、教科書には【正四面体を4等分した三角錐】とか出てくる。
そんなの、ワタシだって想像しきれない。実際に作った今なら判るけど。
てゆか、そんな図、黒板にサラッと書ける教員がいるのか?!
それで、「そっか、うんうん。」て納得する生徒しかいない学級があるのか?!?!
どうやって教えさせ&理解させるつもりで、その問題を作成してるんだ、教科書屋!?
と、言うわけで、
先生方からのリクエストが一番多い、この立体の展開図と組立図をご用意しました。
組立図をクリックすると、別ウィンドウで印刷用のpdfファイルが開きます。

ちなみにこちらの透明バージョンは、特注品です。某KN高校に寄贈しました。
ご要望があれば、製作します。

と言うか、作りたいのでw
そのうちBOOTHに掲載しようかと画策中です。(2024.2月追記)
★ 正四面体の4等分★
正四面体に内接する球は、その正四面体を4等分した三角錐の高さと、半径が等しい。
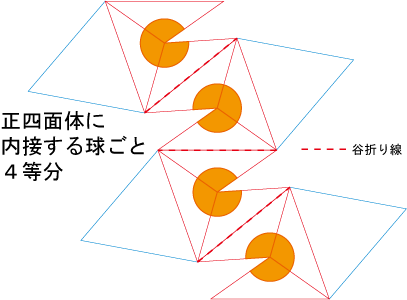
4等分した三角錐の高さ=内接球の半径。
と言うところから、「三角錐の高さって、けっこう低いのカモ?!」と気づきましょう。
上の展開図を、そのまま切り取ってセロテープ等で組み立てると、4つの連なる三角錐ができあがります。
その際、谷折りする線が3本あります。注意してください。
”4つが連なる”バージョンなのは、用紙の都合です。
”ミツウロコ”にしたい場合は、後述の1/4ずつの立体を4つ作って、テープで貼るとイイ感じです。


次は、4つバラバラの組立図です。
同じものを4つ作ると、積み木遊びができます。
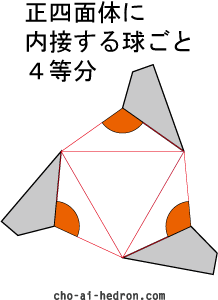
プリンター、A4用紙(厚めだとさらに良い)、はさみ、またはカッター&カッティングボード。
★作り方★
(1)図をクリックすると別ウィンドウでA4サイズのpdfファイルが開くので、印刷します。
(2)黒い太線に沿って、切ります。
(3)細線はすべて山折りにします。
(4)グレーの部分は、みみです。タブです。耳たぶです。
上下それぞれの耳タブの(1)~(5)を順番に重ねながらすべて内側に入れ込むようにして、
組み立てます。角の丸くなっている耳タブを差し込んで、完成です。
普通紙でも、充分にしっかり自立するほどの立体ができるはずです。
それでも強度が心配な場合は、セロテープ等で補強しても良いでしょう。







