★ 三角形ABCの… ★
高校2年の数学の研究授業を見に行ったときに、
どうしても紙の上だけじゃ(ワタシが)理解できないので、勝手に作りました。
問題
鋭角三角形ABCの各辺の中点をそれぞれL、M、Nとし、直線LM、MN、NLで折り曲げて立体を作るとき、
MNの中点Pと、BLの中点Qの距離(PQの長さ)を求めなさい。
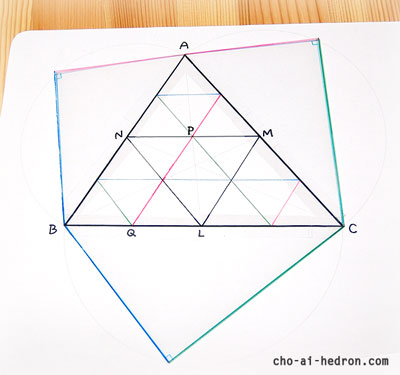
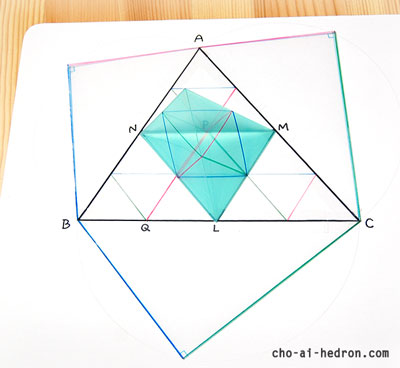
直線LM、MN、NLで折ると、点A、B、Cが、1つの頂点となり、四面体ができあがります。
これを、クリアファイルで作りました。
必要な線を色ペンで書いてから、立体にしています。
解
四面体がぴったり収まる(内接する)直方体を作って、中に入れると、あら不思議!
求めたい距離が一目瞭然!!

このピンクの立体には、PQの長さに該当する部分に、紫色の糸が張ってあります。
この長さは、直方体の高さ(青線の部分)と同じです。
その他にも、MLの中点とBNの中点を結んだ線が緑色の糸、
LNの中点とMAの中点を結んだ線がピンク色の糸で示してあります。
そしてこれらも、直方体の各辺と長さが同じになっています。
三角形の辺の中点と中点を結んだ3本線のがキッチリ直交するって、おもしろーい!!
数学ってなんか不思議で楽しい~♪と、思った瞬間なのでした☆
(2018.5.9 追記)
ところで、数学の先生が「三角形ABCの周りに直角三角形を作ると…」と言う話もしていたので、
最初の厚紙には、三角形ABCの外側に直角三角形が3つあります。
この直角三角形も、それぞれクリアファイルを切り取ったものなので、
AB、BC、CAで折り曲げて立てることができます。
もちろんこれも、四面体になります。一回り大きい四面体です。
大きいほうの四面体の中に、最初の小さい四面体を置いてのぞき込めば、相似関係がよく解ります。
…こんなの紙とペンだけじゃ、理解できませんでしたよー。
ワタシ、進学校の数学にはついていけないみたいですー。
(2017.10.30)


