★ 積分ケーキ ★
積分の問題です。
問題
底面の半径が３の円柱がある。
底面の直径ＡＢを含み、底面と４５°の角をなす平面で円柱を切り取った。
この切り取られた立体の体積を求めよ。
解法
底面の中心Ｏを原点とし、直径ＡＢをｘ軸として、ｘ＝－３からｘ＝３まで積分すればよい。
言うはやすし、ですよねぇ。
そもそも、円柱の半分は想像できるけど、それを４５°で切ったカタチ、想像つく？？
しかもそれ、積分するから、さらに断面形状を考えないといけないのよ？？
お手上げになる生徒、続出まちがいナシです。
もちろん、ワタシだって想像つきませんよ、そんなの。
この問題は、数学のＦ沢先生からの相談でした。
「検索してみたら、生徒の前でダイコンを切って説明する人がいるみたいなんだけど、
毎回、僕がダイコンを持って行って切るのも、悪くはないけど、
そのあとのダイコン、どうするの？職員室で食べるの？？ってｗ」
学校の先生って言うのは、同じ授業を各クラスで行うわけで、
てことは、そのたびにダイコンを食べる羽目になるのですね、それは大変ですよね。
そんなワケで、
包丁とまな板のいらない、
次の授業までに痛んだりしないし、あとでがんばって食べなくてもいい、
そんな教具を作ってみました。
まぁ、円柱ですからね、そこはいいんです。
問題は、カットした状態を、如何にして…何で作るか…どんな風に仕上げるか…
考えながら、展開図を描いて、仮組みをしたところで、
なぜか頭の中に「Happy Birthday♪」が流れてきたので、ケーキになりました。
やっぱりね、見た目がよくないと生徒のノリがよろしくないですからね。
でもまぁ、
【数学の先生が、まな板と包丁を持って教室に現れて、教卓でダイコンを切る！】ほどの
キョーレツさは、ないのですけれど。
えっと。
４５°でカットしたのち、さらに断面形状を考えるにあたって、
ケーキの断面（クリームといちごの層）を、わざと縦にしてあります。
使った素材は、
透明の円柱型ケース、プリントアウトした（ケーキ模様の）型紙、透明板です。
円柱ケースをカットして、断面を透明板で作り、ケーキ模様を内側に入れてあります。
さらにやるなら、おままごとセットみたいに、
スライスの断面をマジックテープでくっつけておくと言う手はあるのですが、
それをやるなら、木材を丸鋸でカットして…みたいなことになって、
家内制手工業では「無理ｗ」と判断しました。
ところで、この問題、
計算方法は、-3から+3までの二等辺三角形断面の積分になるのですが、
元は円柱なのに、計算結果に円周率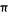
が出てこないんです！
ちょっとびっくりしました。
(2017.10.30)
