★ ヨシモトキューブ No.2★
【ヨシモトキューブ No.2】です。
これの存在を知ったとき、
「『12個の4面体でできる四面体リング2組』・・・え??」
まず、文章を理解するのに時間がかかりました。
と言うか、読んだだけじゃわからないのです。
12個の4面体で、リングが2つ分になるのか、
12個の4面体で構成されるリングが、2つだから、4面体は全部で24個なのか。
文字だけ見ててもわからないので、作るしかない、と思い立ったのです、が。山あり谷ありで。
そもそもの情報は、[宮崎興二著『多面体百科』丸善出版]です。
先ほどの『12個の4面体でできる四面体リング2組』という説明とともに、
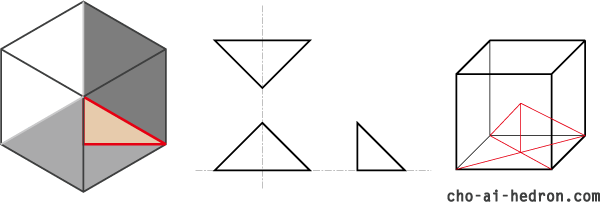
立方体がひし形十二面体に変形する簡単な図があるのですが、
これがまた、それだけでは理解が難しいシロモノでして。
それでもまあ、やるぞ!と意気込んで、ペンを片手に見取り図を描こうとしたのですが・・・
描けない!?
私は機械製図方式で図を描くので、三面図と等角図、必要に応じてキャビネット図を使います。
ヨシモトキューブは【cube】ですからね、立方体から、等分割していって、4面体パーツを描けばいいのです。
が。
この、ヨシモトキューブNo.2のパーツは、描いててとても混乱するんです。
もう、何と言うか、だまし絵なんじゃないか?!と思ってしまうような図になるんです。
キャビネット図が一番マシですね。等角図は最悪ですし、三面図は本当にだまし絵です。
ああ~ヨシモトさん、おそるべし。
と、言うわけで、
よし!これなら!!とココに掲載できる状態になるまでの道のりが、
それはそれで、予想以上に長く楽しく愛おしい時間でございました。
さてさて、こちらが完成品です。

せっかくなので、No.1と並べてみました。
左側が、今回のNo.2です。
でもヨシモトキューブ2は、1枚の写真を見ただけじゃ終わらないんです。
なんと・・・

件の答えは、
【立方体を24等分した、24個の4面体で構成され、その形状は、リング状の立体が2つ。】
なのでした。
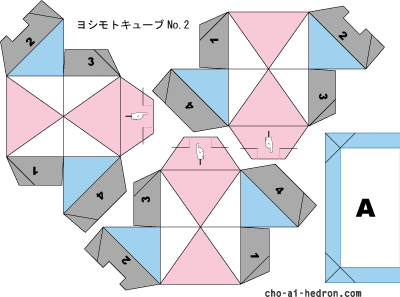
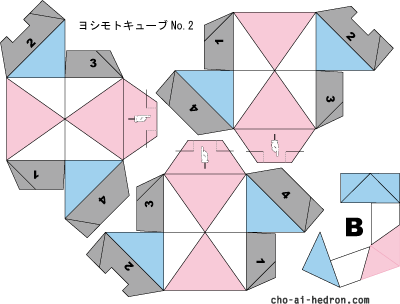
ではいつもの組立図です。
AとBがあります。
メインのパーツは同じですが、おまけパーツがAとBで違います。
それぞれを2枚ずつ印刷してお使いください。
おまけパーツは、それぞれのリングを立方体やひし形十二面体で固定するときに使います。
★難易度【やや高め。】
★接着剤【なくても大丈夫。】
★テープ【テープは必要。マスキングテープだと貼り直しもできてバッチリ。】
パーツ数は全部で【12個】必要です。
1パーツにつき、4面体が2つ分なので、24÷2=12個です。
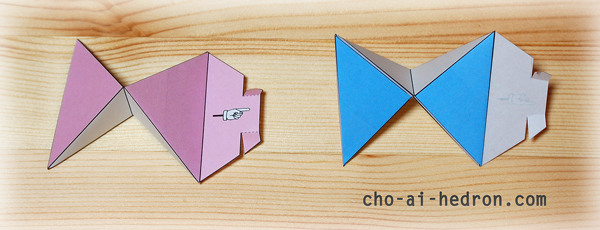
上の写真がパーツの完成図です。
すべて山折りです。
折り目を付けたパーツを、タブの番号順に組み立てます。
指のマークのタブは、切込みを入れて点線を山折りすることで、コネクターになります。
パーツが6個できたら、リングを作ります。
指のマークのタブを、2のタブ部分に差し込んでいくと、中で引っかかって抜けないようになります。
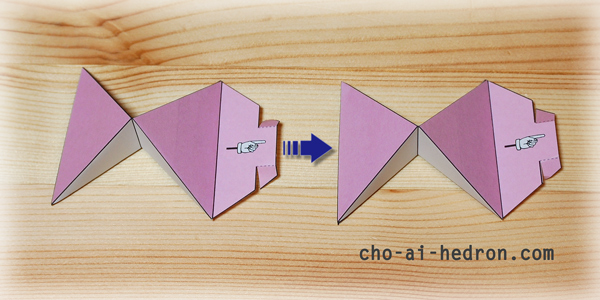
その後、テープでブルーの面だけを補強してください。
ピンクの面は、補強しないほうが、動きはスムーズになります。
リングは2つ用意します。
1日ですべてを作ろうとすると、挫折する可能性が高まるので、
気楽に「今日は3パーツできたぞ☆」と取り組むと良いと思います。
作り方の動画は作成中です☆
立方体からひし形十二面体に変形すると、中に元の立方体と同じ大きさの空間ができます。
するとここに、ヨシモトキューブNo.1がぴったり収まります。
なんともびっくりです。
(2017.8.17)

